私は数学が好きです。

 

・・・ん？？何を急に？？

数学者でもないし、そもそもゼロカーボン（脱炭素）とどんな関わりが？？

と思われた方も多いでしょう。

 

その通り、

数学者のように数学を探求しているわけでもないですし、脱炭素と数学の関連をメチャクチャ理解しているわけでもないです。

 

でも私、

軽い趣味程度に数学の入試問題を解いてみるのが好きで、キレイに解けた際の数学の“美しさ”が好きなのです（変人ですかね・・・）。

 

ということで、今回は、数学好きの私の最近の体験と、（ややこじつけですが）脱炭素と数学の関わりについて、あくまで個人の感想で述べてみたいと思います。

 

＜私の最近の体験＞

2023年春頃、ふと思い立って久しぶりに大学入試問題の問題集をパラパラと眺めてみました。

「入試数学　伝説の良問１００」　安田 亨（講談社ブルーバックス）

「もう一度解いてみる　入試数学」　鈴木 伸介（すばる舎）　etc.

 

　

　　

もちろん、自力で解答できるはずもなく、解法・解説をカンニングするのですが、それを読んでいると「キレイ！」「スマート！」というスッキリ感。

アハ体験的なやつですかね（いや、それとも、変人ですかね・・・）。

加えて、自分が受験生だった頃の「ドキドキ」や「ワクワク（当時は数学が得点源でした）」を思い出しました。

 

 　（ワクワクして仲間を誘いこもうとしているところ）

 

ということで、久しぶりに自分で手を動かして数学の問題を解いてみたい、と気持ちが昂り、勢いそのままに、

数学検定２級（※）　高校２年生レベルまでの数学問題

を申し込んでしまったのです。

 ※https://www.su-gaku.net/suken/examination/summary/2q/
　（出典：公益財団法人　日本数学検定協会より）

 

数学検定２級用の問題集を購入し、いざ、勉強開始！

 

基本的な公式も忘れているので、最初は歯が立たなかったですが、解き始めてみると、公式や解法がとてもキレイだということに、あらためて感動します。

 

・因数分解

・点と直線の距離、円や楕円の方程式

・順列・確率

・相加平均・相乗平均

・三角関数

・微分・積分　etc.

 

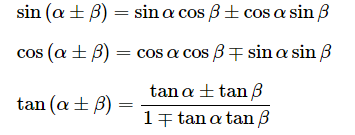
　↑三角関数の公式

 

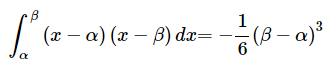
　↑定積分の公式

 

懐かしくないですか？ワクワクしないですか？

・・・しないですよね（苦笑）

 

 
　（ワクワクすることを必死に説明しているが、ちょっと距離を置かれている？）

 

ただ、私は結構ワクワクしておりまして（やっぱり変人）、公式を思い出して暗記したり、そもそもなぜこういう公式が成り立つのか、といったことをあらためて勉強したりしました。

 

「因数分解って、各代数の数式が対称的でキレイ」

「三角関数の公式とか、初めて導いた人すげぇな」

「微分・積分って、画期的な考え方やな」

 

などと思いながら。

 

さて、結果は・・・、３か月前向きに勉強した甲斐もあって、

合格！

“好きこそものの上手なれ“って感じですかね。

 

　

 

 

＜脱炭素と数学＞

という感じで個人的な数学検定体験記でしたが、数学は脱炭素に関わりの深い自然科学の分野でもたくさん応用されているのですよ。

 

ほんの一例かつ私の素人知識なので専門家の方からすると正確ではないかもしれませんが、

・大気中の温度分布や風向風速の予測モデルには微分（厳密には偏微分）の考え方が重要ですし、

・電気や振動などの様々な「波」の物理現象を理解するには、三角関数が強力な武器となりますし、

・当然のことながら、様々なデータ分析において平均・分散・相関等の統計学の考え方は欠かせない

といった感じで、我々の実生活や脱炭素の取り組みの中にも、数学的考え方が非常に大きな役割を果たしているようです。

 

 

自然科学の現象を数学で説明できる、ということは、ゼロカーボンの実現に向けた各種技術検討にも数学的要素が入ってくるよね～、数学ってとても重要な「土台」なんだよね～、

とややこじつけですが思いを馳せながら、今回の記事を締めさせていただきます。

 

数学仲間、求む！

　（あれ？誰もいなくなった・・・）

※本記事は作成者個人の意見や感想に基づき記載しています。
※この記事は2024年5月時点の情報に基づき作成しております。

---

この記事を書いたメンバー

小出 健人

和歌山県出身、趣味は家族旅行で、大学では気象学を専攻。法人のお客さま向けのソリューション企画・運営の全体総括を担当。入社当初から環境問題に興味があり、脱炭素の課題解決に使命感を持って取り組んでいる。本サイトを通して、「地球にありがとう」の気持ちを少しでも広げていけたら、と思っています。

このメンバーが書いた記事を見る